There are several ways to think about coherence; perhaps the simplest, and most relevant here, is the notion that photons that have nearly the same frequency remain more or less in phase with each other over a certain distance, and this distance is inversely correlated with the frequency difference. Light travels at about 300 million meters per second, so a source that has bandwidth of 300 MHz superficially appears to match a distance of 1 meter, but I rather suspect that the usable distance is on the order of ½ of that or less, perhaps even as little as 1/8. (This information is actually easily available on the Web; I’m sure that Dr. Rüdiger Paschotta discusses the issues involved in his superb Encyclopedia. I just haven’t had time to re-familiarize myself with it.)
The gain bandwidth of the laser diode should be specified in its datasheet; unfortunately I can’t find the sheet for my diode on the Web. (The part number is usually given as “S06J”, but I think that’s actually the model of projector that these diodes are taken from.) Judging from the datasheets of other 405-nm laser diodes, I suspect that the bandwidth is perhaps 3 or even 4 nm at reasonable power levels; let’s call it 1% of the wavelength. The center frequency is on the order of 7.5 x 1014 Hz, so the bandwidth amounts to ~7.5 x 1012 Hz.
If you look at ordinary diode lasers you generally find that even at moderate power levels, lots of cavity modes will oscillate. Unless something minimizes the number of oscillating modes, the resulting coherence length is going to be far too short for holography of any ordinary kind. (This is not necessarily the case at low power levels; people have been making very fine holograms with ordinary low-power laser diodes since at least 1999.)
[[Please note that if you see a laser diode described as “single-mode” on eBay, that refers to the transverse mode structure. You want a single transverse mode for holography. If you are intent on buying a laser that is suitable for holography without serious modification, however, you should look for “SLM” or “Single Longitudinal Mode” (or possibly “Single Axial Mode”) in the description, and you should be prepared to pay real money — some nice 532nm SLM lasers show up on eBay from time to time, usually for $2,000 or $3,000...]]
To return to the affordable / DIY side of things:
At least in ordinary red diode lasers, a single cavity mode seems to have bandwidth of perhaps 20 MHz. (I have not seen a figure for 405nm diodes, but I’m not aware of any particular reason to think that it is more than a little different, perhaps by as much as a factor of 2.) Bandwidth of 20 MHz probably represents coherence length of more than 2 meters, which is far better than I need — because my setup is small, I should be able to tolerate bandwidth as high as 200 or 300 MHz. This is still far less than the diode is likely to put out on its own, especially at high power levels, so I have taken steps, as described on the previous two pages, to minimize the number of running modes.
Under ordinary circumstances, people are obliged to do this by decreasing the reflectance of the output facet of the diode chip. They often accomplish this by buying a special diode that is intended for this purpose and already has an anti-reflection coating on its output facet, or by opening up the can and putting a coating on the output facet themselves, which is not exactly trivial. It is then necessary to add external components and use active controls on them in order to achieve and maintain stabilization. The result is an External-Cavity Diode Laser, or ECDL. There are lots of papers about these, and people have even developed mathematical models, which generally suggest that it is very difficult or even impossible to stabilize a laser diode that does not have an AR coating, because the reflection from the output facet provides enough feedback to keep lots of modes oscillating. Moreover, even modest amounts of feedback from external components will often destabilize a laser diode, exactly the opposite of what I want here.
Although these things are correct, it nonetheless seemed to me, after I looked at some of the results obtained by Milan Karakas, that there was at least some chance that I might be able to use an unmodified diode, and that I might be able to use purely passive controls. I must admit that for a while I obtained results that were not very good, some of which were distressingly counterintuitive; but after many hours of fussing and tweaking, I have reached the point where I can now achieve reasonably decent operation (at least with the diode I’m currently using), with coherence length that appears to exceed 25 cm, for periods as long as several minutes. The setup is very tweaky, but that’s not necessarily relevant: I don’t care if I have to adjust the laser in order to be able to make holograms; what I care about is whether I can make holograms at all.
What I’ve done is simple, and may perhaps best be described as a hybrid between an ordinary diode laser and an ECDL; I am providing external feedback in an effort to encourage the diode to operate on only one or a few modes. The nature and amount of feedback are probably slightly different from what people do when they have diodes that are intended for this purpose. That seems quite reasonable to me; there is no reason to expect the usual techniques to apply here.
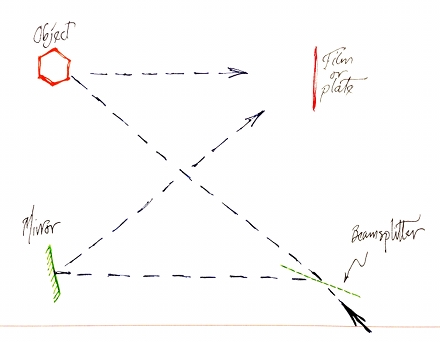
Given the fact that my light source has coherence length of not much more than 2 dozen cm, I have to make sure that the maximum pathlength difference in the holography setup is less than that. My current thought is to use a very simple “X” configuration, so that nearly all of the pathlength differences arise from the fact that the object is not flat. (There are fancier configurations, often used to provide more even illumination of the object, but I don’t need to go there for initial testing.) Here’s a crude diagram:
(For the sake of simplicity, I’ve ignored the fact that the beam is spreading out as it progresses into the setup.)
There is now a subsidiary issue to deal with: the
spacing of the fringes in the hologram depends on the
wavelength and the angle between the reference beam and
the object beam. The equation for this is simple: d, the
space between fringes, is equal to the wavelength
(almost invariably given as λ) divided by the
sine of half of the angle between the beams. I have
drawn the beams about 45° apart in the diagram; that
would result in fringe spacing of only a little more
than 1 micrometer, which is a bit on the small side. I
have some very old film here, which has average grain
size of about 90 nm; 1 μ is only a bit more than 10X
that, and I worry. Either I will avoid that film, or I
will tweak the setup to use an angle of perhaps 22.5 or
30°. (For relatively small angles, the sine is close
to linear; at 30°, the fringes are a little more
than 1.5 μ apart, and at 22.5° they are a little
over 2 μ apart.) The smaller angle would make the
resulting holograms harder to view, but I only hope to
use the old film for initial testing, as holography
films and plates are rather expensive and I don’t
want to waste any more than I must.
The diode I’m using is probably rated for at least 500 mW, and some people have operated this type at 700 mW. At least for now I am restricting mine to about 300 mW, and I lose a fair amount of power along the way, mostly to the interferometers that tell me whether the beam is reasonably coherent; I have not actually measured the output power from the laser table as it goes to the holography platform, but I am hoping that it is at least 100 mW, and possibly as much as 200. I will get some sense of it when I actually try to make holograms: if it takes too long to expose a film or plate, I will probably try turning up the power.
Note: the laser diode is powered by a
“wall-blob” that puts something like 9 V
into a little LM-317T voltage regulator; the output of
the voltage regulator runs into another LM-317T, which
is configured as a current source. This type of cascade
is a technique that a number of diode laser holographers
use to decrease noise and increase stability; it was
suggested to me by Todd Johnson.
About all I’ve done about this so far is to put a washer into the path of the beam, to select the center section and block some of the surrounding noise. That may be enough for initial testing. Eventually, though, I will almost certainly be obliged to put the beam through a spatial filter of some sort. Spatial filters make use of an aspect of lenses that is somewhat less than obvious: in addition to having a focal plane, where it creates an image of the object, a lens also has a Fourier plane, where light that is further from the optical axis correlates with higher spatial frequencies in the object. If you run a laser beam through a lens, and you put a mask at the Fourier plane, you can select various spatial frequencies. If the mask is a pinhole on the axis, you are selecting the lowest spatial frequencies; this is equivalent to saying that you are blocking noise, and letting a clean beam pass through the filter. People usually use a microscope objective and a rather small pinhole, and spatial filters are quite difficult to adjust, but the results are well worth it if you want decent holograms.
Needless to say, however, excluding the [spatial] noise
cuts down the power: any light that doesn’t go
through the pinhole is no longer part of the beam.